Puntos de Lagrange: lugares fijos en el espacio
Una cosa debe quedar clara: nada en el espacio permanece inmóvil. Nada. Desde el pepinazo inicial del Big Bang a la fuerza más básica que representa gravedad todo es un suma y sigue en hacer que el universo sea pura cinética. Luna orbita Tierra, todo el maldito Sistema Solar orbita Tierra y Sol se mueve alrededor del centro de la Vía Láctea, abusando de su campo gravitatorio para arrastrar a todo el Sistema Solar con él.
Chúpate este campo gravitatorio
Sin embargo, existen algunas caprichosas condiciones en las leyes de la física que hacen posible que existan algunos lugares donde las fuerzas de atracción gravitatoria que ejercen dos cuerpos hagan que un tercero permanezca estacionario. Son los Puntos de Lagrange.
Puntos fijos entre dos cuerpos
¿Qué significa estacionario en lenguaje gravitacional? Que su posición respecto al centro de masas no varía. Es decir, que respecto a dos cuerpos más grandes un tercero (siempre de masa despreciable) se mantiene en una posición concreta. Esto representa una solución parcial a lo que se denomina el Problema de los Tres Cuerpos.
Los Puntos de Lagrange son localizaciones en el espacio donde cualquier objeto de masa despreciable respecto a los otros dos tendrá el mismo período orbital que el más pequeño de los dos cuerpos principales y, por tanto, su posición será “fija”.
Sabemos que Tierra orbita Sol; es más, sabemos que la órbita que describe Tierra se completa cada 365 días (aproximadamente). Esto se llama período orbital. Un período orbital depende de la proximidad a la masa principal (al centro de masas). Mercurio gira más rápido porque está más cerca de Sol (además de que recorrer una menor circunferencia), mientras que Marte lo hace más despacio porque está más lejos. En los Puntos de Lagange el período orbital es el mismo que el del cuerpo menor, aunque su órbita sea distinta.
Los planetas y su período orbital
Vamos a ilustrar todo esto con un ejemplo, para esclarecer las dudas. Tomaremos dos cuerpos que conocemos: Tierra y Luna. También podríamos haber optado por Sol y Tierra pero me decanto por una opción más cercana.
El período orbital de Luna es de 28 días (aproximadamente). Bien, los Puntos de Lagrange del sistema Tierra-Luna tendrán un período orbital de 28 días. Esto se debe a que la combinación de las dos fuerzas gravitatorias les conceden la fuerza centrípeta que necesita para que tengan el mismo período orbital que Luna (algo que no debería suceder porque su órbita es distinta a Luna). Voy a dejar la cháchara científica y voy a dónde están. Existen cinco puntos de Lagrange: L1, L2, L3, L4 y L5.
Los cinco Puntos de Lagrange
Para los tres primeros puntos, tened en mente una línea recta que atraviesa Tierra y Luna. Para los dos últimos puntos, L4 y L5, necesitaremos un poco de trigonometría.
- El punto L1 está situado entre Tierra y Luna: su velocidad se ve frenada por la fuerza gravitatoria de Luna; por lo que tiene un período orbital de 28 días.
- El punto L2 está situado más allá de Luna: en esta ocasión, la gravedad de la Luna se opone a la fuerza centrífuga, acelerando el punto hasta un período orbital de 28 días.
- El punto L3 es un poco contradictorio porque está situado en el extremo opuesto a Luna, cerca de Tierra: la suma de las fuerzas gravitatorias de ambos cuerpos (y el hecho de que Tierra también se vea afectada por la gravedad de Luna) hace que tenga el mismo período orbital que Luna.
- El punto L4 está en el vértice de un triángulo equilátero donde Tierra y Luna ocupan los otros vértices. Aquí, las fuerzas combinadas de la gravedad de los dos cuerpos (reducidas cada una de ellas por el ángulo de inclinación de 60º) hacen que el período orbital sea de 28 días.
- El punto L5 está situado en el triángulo simétrico.
Para un mayor esclarecimiento, aquí os dejo un vídeo de 3D4U donde representa un año en el sistema Tierra-Luna. Muy explicativo.
¿Qué utilidad le damos a los Puntos de Lagrange?
Ya tenemos ubicados los Puntos de Lagrange. Muy interesantes. Ahora, ¿cómo podemos incluirlos en nuestra novela de ciencia ficción? Teniendo en cuenta que son puntos fijos entre dos cuerpos de tamaño importante, y que la estabilidad de los puntos se basa en el hecho de tener una masa despreciable, la forma más obvia de darles un uso es mediante la construcción de estaciones espaciales.
Recordemos: los Puntos de Lagrange son las posiciones en las cuales el periodo de rotación en torno al cuerpo mayor es equivalente al período de rotación del cuerpo menor.
Así que, si nos encontramos en el sistema Tierra Luna, el punto L1 sería muy útil como estación de paso a Luna; tal vez como forma de astillero, centro distribuidor de recursos o plataforma de control de un hipotético proceso de colonización a gran escala (incluso terraformación, si se considerara viable convertir esa roca en un mundo con atmmósfera, que lo dudo).
El punto L2 cuenta no es práctico como estación que tenga operaciones comerciales con Tierra, ya que la pérdida de tiempo que supone tener que rodear Luna le resta eficacia; sin embargo, tiene sus ventajas. Al situarse en la cara oculta de Luna L2 se ve significativamente menos afectado por las interferencias del planeta, como la luminosidad artificial o las comunicaciones. Teniendo en cuenta esto, L2 ofrece la posibilidad de ser anfitrión de algún potente sistema de observación del espacio (como un telescopio o un receptor de ondas extrasolares).
El hermano mayor del Hubble podría construirse en L2
Llegando al punto L3 creo necesaria establecer una separación entre los Puntos de Lagrange. En el caso de Tierra-Luna (aunque no exclusivo para este sistema) L1 y L2 no son enteramente estables, requieren de una mínima corrección de rumbo para serlo por completo. Algo que no habría ningún problema para solventar, lo cual no le resta en absoluto valor a esos puntos. Sin embargo, esa mínima corrección de rumbo es algo que los cuerpos celestes no pueden realizar, porque carecen de motores. Por lo que los puntos L1 y L2 están vacantes para ser ocupados por estaciones artificiales. No ocurre lo mismo con los demás puntos.
L3, L4 y L5 son puntos estables, por lo que los microasteroides (poco más que polvo y piedras, aunque peligrosos para cualquier nave) se han ido acumulando allí. Y, en el caso de estar en un sistema habitado por una civilización que domina los viajes espaciales, también nos encontraremos allí basura espacial. Es necesario hacer labores de limpieza antes de poder ocuparlos. Aquí se presentan posibilidades para ser incluidos en vuestra novela.
Se ha perdido contacto con una nave espacial cuya misión era expulsar los escombros de L4. Hay importantes intereses comerciales en juego porque L4 ha sido elegido para albergar una estación de agujero de gusano, cuya emisión de radiación es demasiado peligrosa para situarla en órbita geosincrónica. La reunión para decidir qué hacer es breve: se enviará un segundo equipo a L4. El objetivo es averiguar qué ha sucedido con el primer equipo, pero igual de importante es llevar a cabo las labores de desescombro. Cuando lleguen allí descubrirán que el primer equipo fue destruido por una nave alienígena que había utilizado los escombros de L4 para esconderse de los radares de los terrícolas y poder observar su planeta sin levantar sospechas. ¿Qué mejor lugar para esconder una nave espía? ¿Acaso se han marchado con abundante información sobre las debilidades humanas? ¿Eran una nave pacífica que se vio obligada a destruir al primer equipo para poder escapar? ¿O siguen entre los restos, al acecho? La construcción de esa estación de agujero de gusano acaba de convertirse en una prioridad militar.
Esto es solo un ejemplo. Pero cada uno de vosotros puede darle el uso que quiera a los Puntos de Lagrange.
Iba a terminar el artículo aquí, pero he considerado que, ya que estaba, podría ampliar el artículo con dos elementos más en lo referente a las órbitas de cuerpos celestes: las órbitas geosincrónicas y los asteroides troyanos.
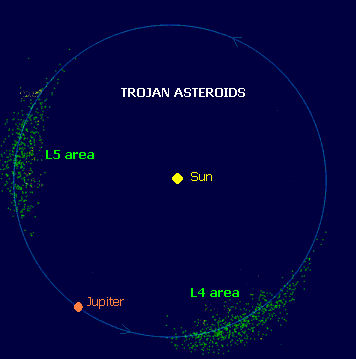
Asteroides troyanos
Son los asteroides que ocupan zonas próximas a los Puntos de Lagrange, en concreto los puntos L4 y L5. Reciben ese nombre porque son una especie de asteroides infiltrados en la órbita de planetas mayores. Describen la misma órbita que el cuerpo menor, aunque no necesariamente en el mismo plano. Aunque en un Punto de Lagrange solo puede haber un único objeto, este punto es muy concreto y específico: a su alrededor proliferan otros asteroides que aunque comparten un período orbital similar (y variable con cada órbita completada) al del cuerpo menor no son en absoluto estables, puesto que también rotan en torno a su órbita, en función de la atracción gravitatoria de los dos cuerpos. En este vídeo se aprecian los asteroides troyanos de Júpiter, localizados cerca de L4 y L5, mayoritariamente. A diferencia de los Puntos de Lagrange, los troyanos no están siempre en el mismo punto, sino en la misma zona. Están inquietos.
Asteroides infiltrados
Órbitas geosincrónicas
Por último, en esta categoría entran todos los objetos, satélites y estaciones que tienen un período orbital en torno a Tierra (o cualquier otro planeta, llegado el caso) igual al período de rotación del planeta (en nuestro caso, 24 horas). Si miráramos al cielo con un telescopio podríamos verlos siempre sobre nosotros, independientemente de si es día o noche. La órbita geoestacionaria es un tipo muy concreto de órbita geosincrónica, la que está sobre la línea del ecuador.
Los ejemplos más habituales de satélites geosincrónicos y geoestacionarios son los de observación meteorológica (el famoso METEOSAT) pero hay otros muy interesantes que podrían estar en órbita geosincrónica, como por ejemplo un ascensor espacial, del que os hablaré en otra entrada.




No hay comentarios:
Publicar un comentario